Measure-Theoretic Reeb Graphs and Reeb Spaces
Discrete & Computational Geometry, 2025
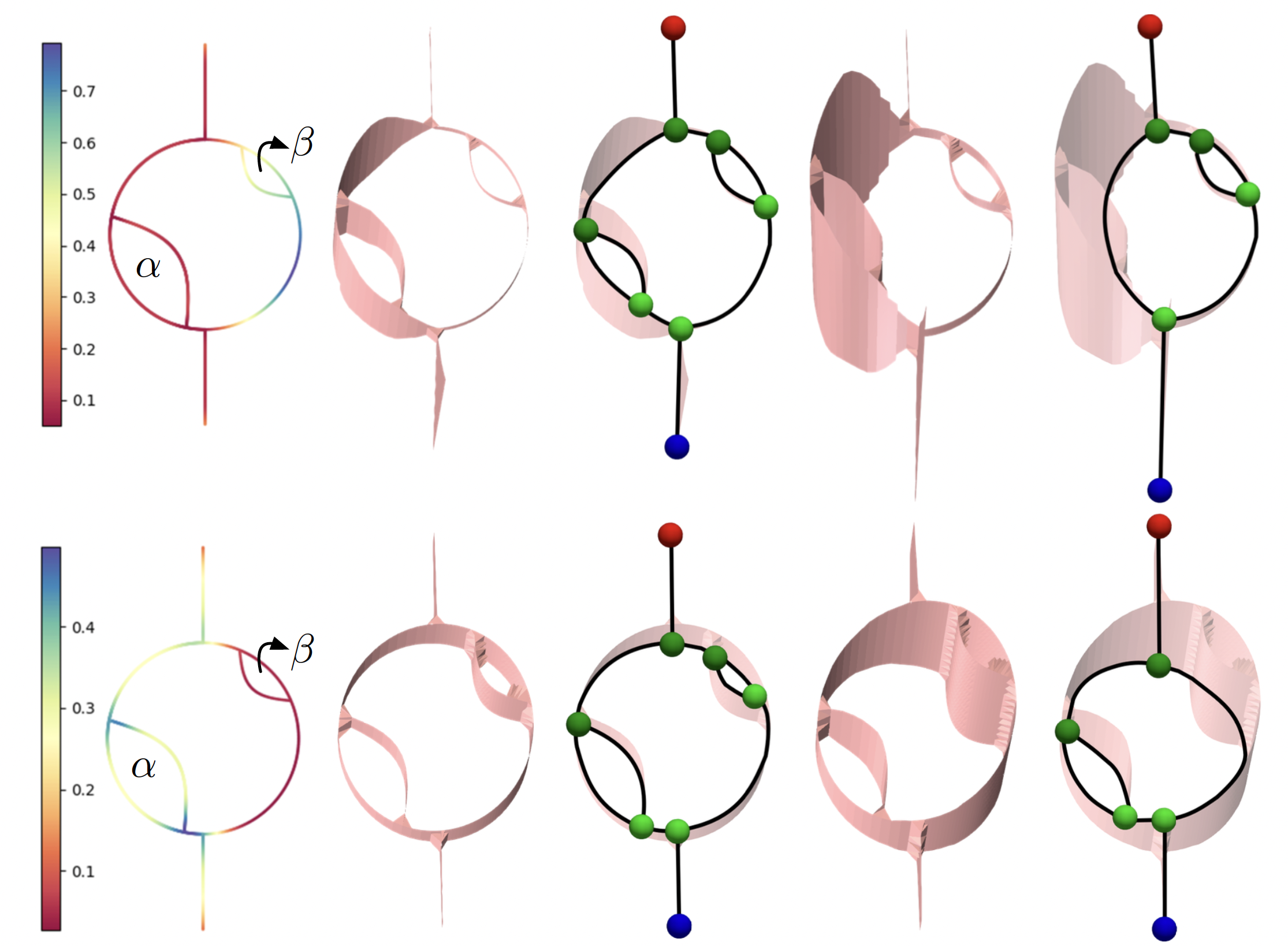
Abstract:
A Reeb graph is a graphical representation of a scalar function on a topological space that encodes the topology of the level sets. A Reeb space is a generalization of the Reeb graph to a multiparameter function. In this paper, we propose novel constructions of Reeb graphs and Reeb spaces that incorporate the use of a measure. Specifically, we introduce measure-theoretic Reeb graphs and Reeb spaces when the domain or the range is modeled as a metric measure space (i.e., a metric space equipped with a measure). Our main goal is to enhance the robustness of the Reeb graph and Reeb space in representing the topological features of a scalar field while accounting for the distribution of the measure. We first introduce a Reeb graph with local smoothing and prove its stability with respect to the interleaving distance. We then prove the stability of a Reeb graph of a metric measure space with respect to the measure, defined using the distance to a measure or the kernel distance to a measure, respectively.
Download Paper DOI
To cite: Qingsong Wang and Guanqun Ma and Raghavendra Sridharamurthy and Bei Wang "Measure-Theoretic Reeb Graphs and Reeb Spaces" Discrete and Computational Geometry 10.1007/s00454-025-00789-4
BibTeX:
@article{WangetalDCG2025, title={Measure-Theoretic Reeb Graphs and Reeb Spaces}, author={Wang, Qingsong and Ma, Guanqun and Sridharamurthy, Raghavendra and Wang, Bei}, journal={Discrete \& Computational Geometry}, pages={1--26}, year={2025}, publisher={Springer US} } 